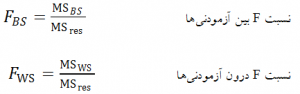تحلیل واریانس دوطرفه یا طرح دو عاملی (Two–Way ANOVA)
در تحلیل واریانس دوطرفه تأثیر دو متغیر (دو عامل) به طور همزمان مورد مطالعه قرار میگیرند که در آن ترکیبهای مختلفی از سطوح دو متغیر وجود دارد. برای مثال آیا تاثیر جنسیت (پسر و دختر) بر اضطراب امتحان به مقطع تحصیلی (ابتدایی و متوسطه) آنها بستگی دارد؟ در این پژوهش یک متغیر وابسته کمی و دو متغیر مستقل یا عامل یعنی مقطع تحصیلی و جنسیت وجود دارد که هر یک از آنها دارای دو سطح است. به آزمون مورد استفاده برای چنین پژوهشهایی تحلیل واریانس دو طرفه یا دو عاملی گفته میشود.
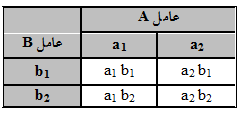
به طور کلی اگر متغیر A دارای p سطح و متغیر B نیز دارای q سطح باشد، طرح مورد نظر یک طرح عاملی q×p نامیده میشود. رایجترین نوع تحلیل واریانس عاملی طرح ۲×۲ است که در آن دو متغیر مستقل وجود دارد که هر کدام دو سطح دارند. در جدول زیر یک طرح ۲×۲ نشان داده شده است.
طرح عاملی ۲×۲
پیش فرضهای تحلیل واریانس دوطرفه
۱– متغیر وابسته باید کمی (فاصلهای یا نسبی) باشد.
۲- دو متغیر مستقل یا عامل حداقل با دو سطح وجود داشته باشد. یعنی مقیاس آنها سطح اسمی یا رتبهای باشد.
۳- گروهها مستقل از یکدیگر و واریانس آنها برابر باشد.
۴- توزیع دادهها نرمال باشد.
فرضیههای تحلیل واریانس دوطرفه
با انجام تحلیل واریانس دوطرفه، سه فرضیه مورد بررسی قرار میگیرد و سه نتیجه حاصل میشود:
- اثر اصلی متغیر مستقل اول (عامل A) بر متغیر وابسته
- اثر اصلی متغیر مستقل دوم (عامل B) بر متغیر وابسته
- اثر متقابل یا تعامل دو متغیر مستقل بر روی متغیر وابسته. اثر تعاملی بررسی میکند که آیا اثر یک عامل بر متغیر وابسته به اینکه چه سطحی از عامل دیگر اجرا شده باشد، بستگی دارد یا خیر؟
فرضیههای صفر و خلاف به صورت زیر تدوین میشوند:


محاسبه نسبت F در تحلیل واریانس دوعاملی


تصمیمگیری: در صورتی که F محاسبه شده هر یک از عوامل (A، B و اثر تعاملی AB) از F بحرانی جدول بزرگتر یا مساوی باشد (یا ۰٫۰۵ > p-value)، فرض صفر رد و فرض خلاف تأیید میشود. بنابراین اگر فرض خلاف درباره هر یک از عاملها تأیید شود، با اطمینان ۹۵ درصد میتوان نتیجه گرفت اثر اصلی هر یک از عاملها (یعنی اثر اصلی A و اثر اصلی B) و اثر تعاملی A و B بر متغیر وابسته معنیدار است یا به عبارت دیگر تأثیر آنها پذیرفته میشود.
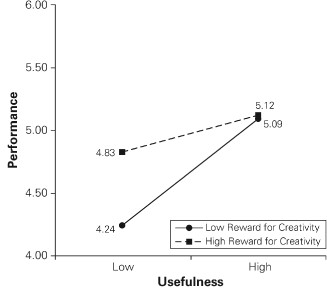
استفاده از نمودار برای نمایش اثرهای تعاملی
در تحلیل واریانس دوطرفه با استفاده از نمودار میتوان وجود یا عدم وجود اثر تعاملی بین متغیرها را نشان داد.
– در نمودار تعامل، شیب هر یک از خطوط تا حدودی بیانگر میزان ارتباط بین دو متغیر است. هر چه شیب خط زیادتر باشد، ارتباط بین متغیرها بیشتر است.
– اگر خطوط نمودار یکدیگر را قطع کنند، در اینصورت اثر تعاملی را نامنظم میگویند. یعنی سطوح عامل A روی سطوح عامل B تأثیر متفاوت دارد.
– اگر دو خط موازی باشند، تعامل آنها بی معنی یا صفر است. به عبارتی تعامل B× A صفر است. یعنی میزان ارتباط برای هر دو سطح تقریباً یکسان است.
– اگر خط نمودار موازی محور Xها باشد، نشانه نبود ارتباط است. اگر دو خط نمودار موازی یکدیگر نباشند و یکدیگر را نیز قطع نکنند، اثر تعاملی را منظم میگویند.