آزمونهای پارامتریک برای فرضیههای همبستگی و رابطه ای
آزمون های همبستگی برای بررسی رابطه بین دو یا چند متغیر به کار میروند. همبستگی به معنای همتغییری دو متغیر است که از آن استنباط میشود افزایش یا کاهش یک متغیر با افزایش یا کاهش متغیر دیگر همراه است. به عنوان مثال، بین هوش و پیشرفت تحصیلی دانشآموزان رابطه مستقیم وجود دارد. یعنی هر چه هوش دانشآموزان بیشتر باشد، نمره پیشرفت تحصیلی آنها نیز افزایش مییابد. آزمون های همبستگی به دو دسته آزمون های پارامتریک و ناپارامتریک تقسیم میشوند. در صورتی که مقیاس متغیرها فاصله ای یا تسبی و توزیع متغیرها نرمال باشد، از آزمون های همبستگی پارامتریک مانند آزمون همبستگی پیرسون و در غیر این صورت از آزمون های همبستگی ناپارامتریک استفاده میگردد.
آزمون همبستگی پیرسون (Pearson Correlation Coefficient)
- ضریب همبستگی برای توصیف شدت رابطه بین متغیرها به کار میرود.
- رابطه علت و معلولی را نمیتوان از همبستگی استنباط کرد. یعنی میتواند متغیر سومی وجود داشته باشد که ارتباط بین دو متغیر مورد مقایسه را توصیف کند. برای مثال، تحقیقات نشان میدهد بین اضطراب مادران و یادگیری کودکان رابطه معکوس وجود دارد. ممکن است کاهش یادگیری کودک و اضطراب مادر ناشی از علل دیگری مانند درآمد پایین خانواده، مشکلات ژنتیکی و غیره باشد
- گاهی بین متغیرها همبستگی ساختگی، مصنوعی یا مجازی وجود دارد. درحالیکه احتمالاً رابطه و قطعاً رابطه علی بین آنها وجود ندارد. برای مثال بین هوش و رنگ چشم افراد همبستگی وجود دارد.
- همچنین همبستگیای که در یک نمونه قابل ملاحظه است، ممکن است در نمونه دیگر معادل صفر باشد.
ضریب همبستگی پیرسون، جزء آزمونهای آماری پارامتریک محسوب میشود که نشان دهنده درجه رابطه خطی بین دو متغیر است و توسط کارل پیرسون ارائه شده و آن را با حرف r نشان میدهند. مقدار آن بین دو عدد ۱+ و ۱- تغییر میکند. مقدار قدر مطلق ضریب همبستگی، شدت یا درجه رابطه بین دو متغیر و علامت آن (مثبت یا منفی) جهت رابطه (مستقیم یا معکوس) را نشان میدهد. ضریب همبستگی پیرسون یک شاخص متقارن است. یعنی همبستگی بین متغیرهای X و Y با همبستگی بین متغیرهای Y و X برابر است.
پیش فرضهای ضریب همبستگی پیرسون
استفاده از ضریب همبستگی پیرسون مستلزم پیش فرضهای زیر است:
- مقیاس متغیرها حداقل فاصلهای باشد.
- توزیعها تقریباً نرمال باشند.
- رابطه بین دو متغیر خطی باشد. نمودار پراکندگی، ساده ترین روش برای بررسی خطی یا غیرخطی بودن رابطهی بین متغیرها میباشد.
- شرط یکسانی واریانسها رعایت شود. به عبارت دیگر، باید نمودار پراکندگی یکسان باشد. به این معنی که عرض نقاط در سرتاسر نمودار یکسان باشد.
فرمول محاسبه ضریب همبستگی پیرسون

حالتهای مختلف همبستگی
در مطالعه همبستگی با حالتهای مختلفی مواجه میشویم. حالتهای مختلف همبستگی بین متغیرها و نمودار پراکنش آنها عبارتند از:
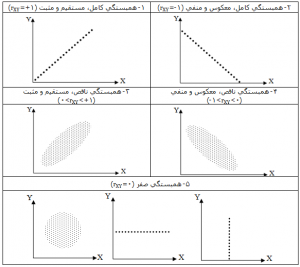
شدت یا درجه همبستگی. در صورتیکه ضریب همبستگی محاسبه شده معنیدار باشد، هر چه مقدار قدر مطلق آن پایین و نزدیک صفر باشد، رابطه ضعیف و هرچه بالاتر و نزدیک ۱ باشد، رابطه قویتر است.
ضریب تعیین. میزان اشتراک تغییرات، درصد پراکندگی یا واریانس مشترک بین دو متغیر را تعیین میکند. با محاسبه این ضریب میتوان تعیین کرد که چند درصد از کل واریانس X ناشی از واریانس Y است. هر چه این درصد بالاتر باشد به طور قطع رابطه قویتر خواهد بود.
ν=(r)۲×۱۰۰
به عنوان مثال اگر شدت همبستگی بین دو متغیر ۰٫۵۴ باشد (۰٫۵۴=r)، ضریب تعیین برابر است با
ν=(۰٫۵۴)۲×۲۹= ۱۰۰
یعنی متغیر X، حدود ۲۹ درصد واریانس Y را تبیین میکند.
نکته :
1) صفر بودن ضریب همبستگی تنها عدم وجود رابطه ی خطی بین دو متغیر را نشان می دهد ولی نمی توان مستقل بودن دو متغیر را نیز نتیجه گرفت. هنگامی که ضریب همبستگی پیرسون بین دو متغیر صفر باشد، این متغیرها تنها در صورتی مستقل از یکدیگرند که توزیع متغیرها نرمال باشد.
2) همبستگی بین دو متغیر تنها نشان دهنده ی این است که افزایش یا کاهش یک متغیر چه تاثیری بر افزایش یا کاهش متغیر دیگر دارد ولی این همبستگی ضرورتا دال بر رابطه ی علّی بین متغیرها نمی باشد. به طور مثال اگر در یک تحقیق دو متغیر قد و تحصیلات همبستگی مثبت بالایی داشته باشندنمی توانیم نتیجه بگیریم که افراد قد بلندتر دارای تحصیلات بیشتری هستند. بنابراین باید بین مفاهیم همبستگی و رابطه ی علّت و معلولی تفاوت قائل شد. به بیان دیگر ممکن است دو متغیر همبستگی داشته باشند ولی لزومی ندارد که یکی از متغیرها علت و دیگری معلول باشد، علاوه براین عوامل متعدد دیگری نیز می توانند بر ضریب همبستگی اثرگذار باشند.